7 алгоритама које сваки програмер треба да зна

Као студент програмирања, вероватно сте током своје каријере научили много различитих алгоритама. Познавање различитих алгоритама је апсолутно неопходно за сваког програмера.

Са толико алгоритама, може бити изазов пратити шта је битно. Ако се припремате за интервју или једноставно надопуните своје вештине, ова листа ће вам бити релативно лака. Читајте даље док наводимо најважније алгоритме за програмере.

1. Дијкстрин алгоритам

Едсгер Дијкстра био је један од најутицајнијих компјутерских научника свог времена и дао је свој допринос много различитих области рачунарске науке, укључујући оперативне системе, конструкцију компајлера и још много тога више. Један од најзначајнијих доприноса Дијкстре је генијалност његовог алгоритма за најкраћи пут за графиконе, познатог и као Дијкстрин најкраћи алгоритам путање.

Дијкстрин алгоритам проналази најкраћу путању у графикону од извора до свих врхова графа. На свакој итерацији алгоритма додаје се врх са минималном удаљеношћу од извора и оним који не постоји на тренутној најкраћој путањи. Ово је похлепно својство које користи Дјикстрин алгоритам.

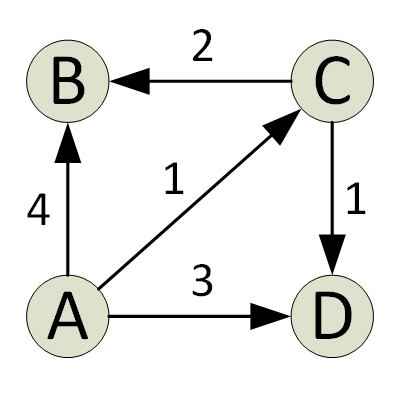
Алгоритам се обично примењује помоћу скупа. Дијкстрин алгоритам је веома ефикасан када се имплементира са минималном количином; можете пронаћи најкраћи пут за само О (В+ЕлогВ) време (В је број темена, а Е број ивица у датом графикону).

Дијкстрин алгоритам има своја ограничења; ради само на усмереним и неусмереним графовима са ивицама позитивне тежине. За негативне тежине, типично је пожељан Беллман-Форд алгоритам.

Питања за интервју обично укључују Дјикстрин алгоритам, па топло препоручујемо да разумете његове замршене детаље и апликације.

2. Сортирање спајањем

На овој листи имамо неколико алгоритама за сортирање, а сортирање спајањем је један од најважнијих алгоритама. То је ефикасан алгоритам сортирања заснован на техници програмирања Дивиде анд Цонкуер. У најгорем случају, сортирање спајањем може сортирати „н“ бројеве за само О (нлогн) време. У поређењу са примитивним техникама сортирања као што су Буббле Сорт (за то је потребно О (н^2) време), сортирање спајањем је изузетно ефикасно.

Повезан: Увод у алгоритам сортирања споја

У сортирању спајањем, низ који се сортира се непрестано разбија у подмасе све док се сваки подниз не састоји од једног броја. Рекурзивни алгоритам затим више пута спаја подмазе и сортира низ.

3. Куицксорт

Куицксорт је још један алгоритам сортирања заснован на техници програмирања Дивиде анд Цонкуер. У овом алгоритму, елемент се прво бира као заокрет, а цео низ се затим партиционира око овог заокрета.

Као што сте вероватно претпоставили, добар заокрет је пресудан за ефикасно сортирање. Окретни елемент може бити или случајни елемент, медијски елемент, први елемент или чак последњи елемент.

Имплементација брзог сортирања често се разликује по начину на који бирају заокрет. У просечном случају, брзо сортирање ће сортирати велики низ са добрим заокретом за само О (нлогн) време.

Општи псеудокод брзог сортирања опетовано партиционира низ на заокрету и поставља га у исправну позицију подмазе. Такође поставља елементе мање од пивота лево и елементе веће од пивота десно.

4. Дубинска прва претрага

Дептх Фирст Сеарцх (ДФС) је један од првих алгоритама графикона који се учи студентима. ДФС је ефикасан алгоритам који се користи за кретање или претраживање графикона. Такође се може модификовати за употребу при преласку стабала.

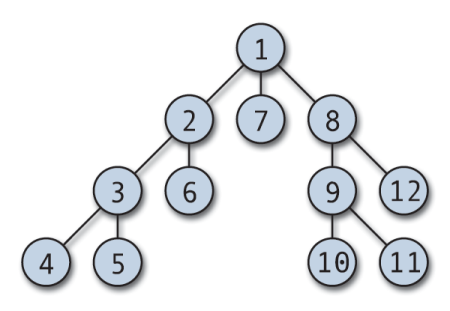
ДФС прелазак може започети са било ког произвољног чвора и рони у сваки суседни врх. Алгоритам се враћа уназад када нема непосјећеног врха или постоји слијепа улица. ДФС се обично примењује са стеком и логичким низом за праћење посећених чворова. ДФС је једноставан за имплементацију и изузетно ефикасан; ради (В+Е), где је В број темена, а Е број ивица.

Типичне примене ДФС преласка укључују тополошко сортирање, откривање циклуса у графикону, проналажење путање и проналажење снажно повезаних компоненти.

5. Претрага у ширину

Бреадтх-Фирст Сеарцх (БФС) је такође познат као прелаз по нивоу за дрвеће. БФС ради у О (В+Е) слично ДФС алгоритму. Међутим, БФС користи ред уместо гомиле. ДФС понире у графикон, док БФС прелази граф по ширини.

БФС алгоритам користи ред за праћење врхова. Непосећена суседна темена се посећују, обележавају и стављају у ред. Ако тачка нема суседних тачака, онда се тачка уклања из реда и истражује.

БФС се обично користи у пеер-то-пеер мрежама, најкраћој путањи непондерисаног графа и за проналажење минималног распона стабла.

6. Бинари Сеарцх

Бинари Сеарцх је једноставан алгоритам за проналажење потребног елемента у сортираном низу. Ради тако што се низ непрекидно дели на пола. Ако је тражени елемент мањи од крајњег елемента, онда се лева страна средњег елемента даље обрађује; у супротном, десна страна се преполовљује и поново претражује. Поступак се понавља све док се не пронађе потребан елемент.

Сложеност бинарног претраживања у најгорем случају је О (логн) што га чини врло ефикасним у претраживању линеарних низова.

7. Алгоритми минималног распона стабала

Минимално распонско стабло (МСТ) графикона има минималне трошкове међу свим могућим распонским стаблима. Цена разапињућег дрвета зависи од тежине његових ивица. Важно је напоменути да може постојати више од једног минималног стабла. Постоје два главна МСТ алгоритма, наиме Крускалов и Примов.

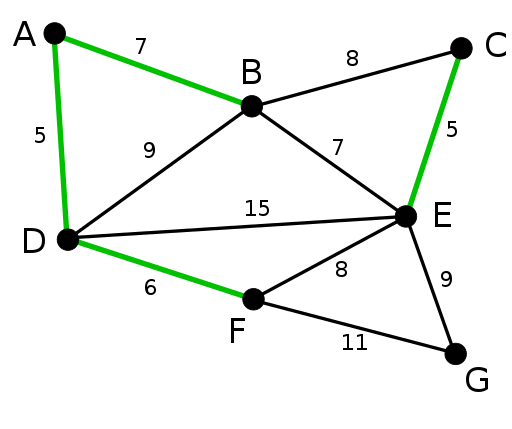
Крускалов алгоритам ствара МСТ додавањем ивице са минималним трошковима растућем скупу. Алгоритам прво сортира ивице према њиховој тежини, а затим додаје ивице у МСТ почевши од минимума.

Важно је напоменути да алгоритам не додаје ивице које чине циклус. Крускалов алгоритам се преферира за ретке графиконе.

Примов алгоритам такође користи похлепно својство и идеалан је за густе графиконе. Централна идеја Прим -овог МСТ -а је да има два различита скупа врхова; један скуп садржи растући МСТ, док други садржи неискоришћене врхове. На свакој итерацији бира се ивица минималне тежине која ће повезати два скупа.

Алгоритми минималног распона стабла неопходни су за кластер анализу, таксономију и мреже за емитовање.

Ефикасан програмер добро познаје алгоритме

Програмери непрестано уче и развијају своје вештине, а постоје неке основне ствари у којима сви морају бити вешти. Вешт програмер зна различите алгоритме, предности и недостатке сваког од њих и који би алгоритам био најприкладнији за дати сценарио.

Увод у алгоритам сортирања љуске

Иако сортирање љуске није најефикаснији метод, почетници имају много користи од вежбања.

Прочитајте следеће

О аутору