Шта је бинарно? [Објашњена технологија]

Реклама

С обзиром на то да је бинарни систем тако апсолутно важан за постојање рачунара, чини се чудним да га никада нисмо решили тема раније - па сам данас мислио да ћу дати кратак преглед шта бинарно заправо значи и како се користи у рачунари. Ако сте се увек питали у чему је разлика између њих 8-битни, 32-битни, и 64-битни заиста јесте, и зашто је то важно - читајте даље!

Шта је бинарно? Разлика између базе 10 и базе 2

Већина нас је одрасла у базном свету бројева 10, под тим што мислим да их имамо 10 'База' бројеви (0-9) из којих добијамо све остале бројеве. Након што смо их исцрпили, прелазимо на ниво јединице - 10, 100, 1000 - овај облик бројања уроњен је у наш мозак од рођења. У ствари, тек из римског периода започели смо бројање у бази 10. Прије тога, база 12 била је најлакша, а људи су користили бродове да би рачунали.

Када у основној школи учимо базу 10, често пишемо јединице попут ове:

Дакле број 1990 се у ствари састоји од 1 к 1000, 9 к 100, 9 к 10, и 0 к 1. Сигурна сам да не треба даље објашњавати базу 10.

Али шта ако уместо потпуног избора 0,1,2,3,4,5,6,7,8,9 да радимо са основним бројевима - шта ако имамо 0, и 1. Ово се зове база 2; а такође се обично назива бинарни. У бинарном свету можете само да рачунате 0,1 - тада морате прећи на следећи ниво јединице.

Бројање у Бинарном

Изузетно помаже ако напишемо јединице приликом учења бинарног записа. У овом случају, уместо да се свака додатна јединица помножи са 10, помножи се са 2, што даје нама 1,2,4,8,16,32,64 … Дакле, да бисмо лакше израчунали, можемо их овако записати:

Другим речима, највећа вредност у бинарном броју представља колико је 1. Следећа цифра, лево од тога, представља колико су 2. Следећи представља колико 4 је… и тако.

С тим знањем можемо написати табелу бројања у бинарним форматима, са левом еквивалентном основном вриједношћу 10.

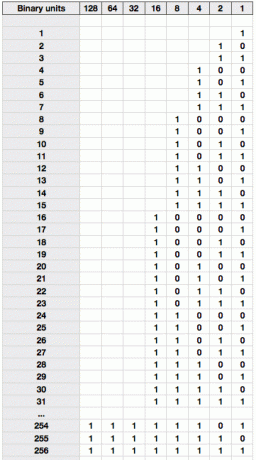
Проведите тренутак преко тога док не будете тачно видели зашто је 25 написано као 11001. Требали бисте бити у стању да га разбијете као 16 + 8 + 1 = 25.

Рад уназад - база од 10 до бинарних података

Сада бисте могли да схватите која вредност има бинарни број цртањем сличне табеле и множењем сваке јединице. За пребацивање регуларног броја 10 на бинарни потребно је мало више напора. Први корак је проналажење највеће бинарне јединице која се "уклапа" у број. На пример, ако смо радили 35, тада је највећи број из те табеле који се уклапа у 35, па бисмо у тој колони имали 1. Затим имамо остатак 3 - коме би била потребна 2, а на крају и 1. Тако смо добили 100011.

8-бита, бајтова и октета

Табела коју сам приказао горе је 8-битна, јер имамо максимално 8 нула и оне које користимо за наш бинарни број. Дакле, максимални број који евентуално можемо да представимо је 11111111, или 255. То је разлог зашто би се могао представити било који број из 0-255, треба нам најмање 8 бита. Октет и Бајт је једноставно још један начин казивања 8-битних. Стога 1 бајт = 8 бита.

32 у односу на 64-битна рачунарства

Данас често чујете изразе 32-битне и 64-битне верзије Виндовс-а и можда знате да 32-битни Виндовс може да подржава само ону до 4 гигабајта РАМ-а. Зашто је то?

Све се своди на адресирање меморије. Сваком залогају меморије потребна је јединствена адреса како би јој се приступило. Да смо имали 8-битни система за адресирање меморије, могли бисмо да имамо само највише 256 бајтова меморије. Са 32-битни систем за адресирање меморије (замислите да проширите горњу табелу да бисте имали 32 колона бинарних јединица), можемо ићи било где до горе 4,294,967,296? 4 милијарде бајтоваили другим речима - 4 ГИГАбајтова.64-битни рачунарство у основи уклања ово ограничење тако што нас издаје 18 куинтиллион различите адресе - неки од нас већина једноставно не може схватити.

ИПв4 Адресирање

Све је последња брига у свету рачунара о ИП адресама ИПв6 и долазак АРПАгеддон [Објашњена технологија] Опширније , нарочито ИПв4 адресе попут ових:

• 192.168.0.1
• 200.187.54.22

У ствари се састоје од 4 броја, од којих сваки представља вредност до 255. Можете ли погодити зашто? Да, целу адресу представља 4 октета (32 бита укупно). Ово је изгледало као јако пуно могућих адреса (у ствари око 4 милијарде) у време кад је интернет први пут измишљен, али сада нам брзо нестаје када све у нашем животу треба бити повезано. Да би се то решило, користи се нови ИПв6 128 бита укупно, дајући нам отприлике 340 ундециллион (ставите 38 нула на крај) адресе за играње.

Оставицу га данас за данас, тако да могу да се вратим свом првобитном циљу који је био писање следецег Ардуиновог туторијала - у коме обимно користимо регистар мало смена. Надам се да сам вам данас дао основно разумевање колико је бинарни значај тако значајан за рачунаре, зашто се исти бројеви и даље појављују и зашто је број битова које морамо да представљамо поставља ограничено ограничење количине меморије, величине екрана, могућих вредности боја или јединствених ИП адреса које су нам доступне. Следећи пут ћемо погледати бинарне логичке прорачуне, што је поприлично све што ради рачунарски процесор, као и како рачунари могу представљати негативне бројеве.

Коментари? Конфузија? Да ли сте сматрали да је моје објашњење лако разумети? Без обзира на случај, обратите се коментарима. Оставићу вас са бинарном шалом!

На свету постоји само 10 типова људи: они који разумеју бинарнии оне који то немају.

Кредитна слика: Схуттерстоцк